EV3でハノイの塔を　その４ - The Fool In The Valleyの雑記帳

THS1のプログラムを書く前に、ハノイの塔の解法を整理します。今回はEV3に直接には関係のない、一般的な話です。

ーーーーーーーーーーーーーーーー

ハノイの塔と呼ばれるパズルは写真のようなもので、そのルールは次の通りである。

f:id:tfitv:20210224140207j:plain

3本の柱と中央に穴の開いた大きさの異なる円盤があり、初期状態は円盤は左の柱に重なっている。
円盤を一度に一枚ずつ移動させ、全ての円盤を右の柱に移動させる。
ただし、大きい円盤を小さい円盤の上に置くことはできない。

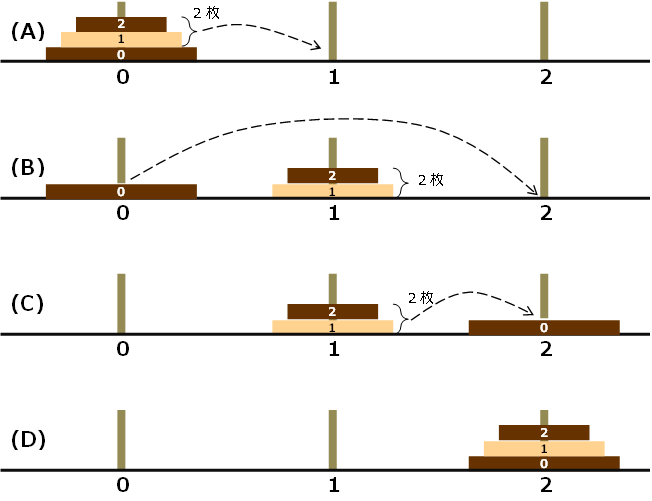
一般的な解法を考えるために、先ず下の図のように3枚の円盤が重なった場合を考える。ここで、便宜上、左の柱を0，中の柱を1，左の柱を2という番号で区別しておく。初期状態（A)から最終状態（D)に変えるためには、(A)のように柱０にある上の2枚を何らかの処理によって柱１に移動させ、(B)のように柱０に残った一番大きな円盤０を柱２に移したあと、今度は(C)のように柱１にある2枚を何らかの処理によって柱２に移動させればいいことがわかる。

f:id:tfitv:20210224113816p:plain

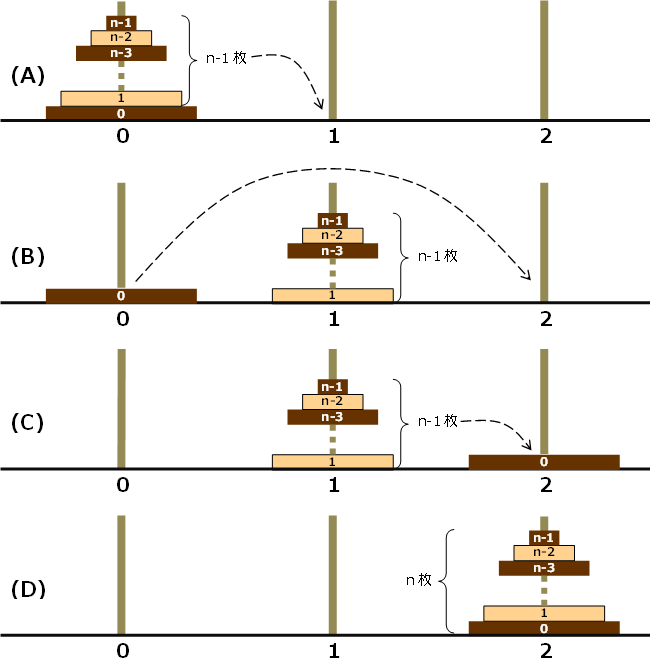
これを一般化してn枚の円盤の場合を考えてみる。ここで、初期状態で動かしたい円盤がある柱を初期の柱、最終状態でそれらの円盤が移動した柱を最終の柱、もう一つの柱を補助の柱と呼ぶことにする。初期状態（A)から最終状態（D)に変えるためには、まず(A)のように初期の柱にある上のn-1枚を何らかの処理によって補助の柱に移動させる。次に(B)のように初期の柱に残った一番大きな円盤０を最終の柱に移す。最後に今度は(C)のように補助の柱にあるn-1枚を最終の柱に移動させればよい。同様に、n-1枚を動かすためには、それが刺さった柱を初期の柱として、そこの上のn-2枚を補助の柱に動かし、残った一番大きな円盤1を最終の柱に移したあと、今度は補助の柱にあるn-2枚を最終の柱に移動すると考えればよい。この考え方を繰り返し、n-2枚を動かすためには・・・という作業を続け、動かしたい円盤が1枚になるまで繰り返す。

f:id:tfitv:20210223223333p:plain

この解法をPythonでプログラム化することを考える。初期の柱scにあるn枚の円盤を目的の柱dcに移動する処理を再帰的な関数solve(n, sc, dc) で定義すると、アルゴリズムは次のような簡単なプログラムで記述することができる。ここで、3本の柱を０，１，２の番号で区別しておくと、3-sc-dcには、初期でも最終でもない補助の柱の番号がセットされる。

def solve(nt, n, sc, dc):
    if n > 1:
        solve(nt, n-1, sc, 3-sc-dc)
    moveBottomDisc(nt, n, sc, dc)   #残った一番下の円盤を目的柱に移動する処理
    if n > 1:
        solve(nt, n-1, 3-sc-dc, dc)

def moveBottomDisc(nt, n, sc, dc):
    print('円盤', nt-n, 'を柱',sc , 'から柱', dc, 'に移動する')

nt=3
n=nt
solve(nt, n, 0, 2)

このPythonプログラムをhanoi.pyとして実行すると結果は、次のようになる。

D:\Dev\MyPythonProject>python hanoi.py
円盤 2 を柱 0 から柱 2 に移動する
円盤 1 を柱 0 から柱 1 に移動する
円盤 2 を柱 2 から柱 1 に移動する
円盤 0 を柱 0 から柱 2 に移動する
円盤 2 を柱 1 から柱 0 に移動する
円盤 1 を柱 1 から柱 2 に移動する
円盤 2 を柱 0 から柱 2 に移動する

再帰的な呼び出しは、その流れを図で表現すると理解しやすい。上記の円盤が3枚の例は次のようになる。

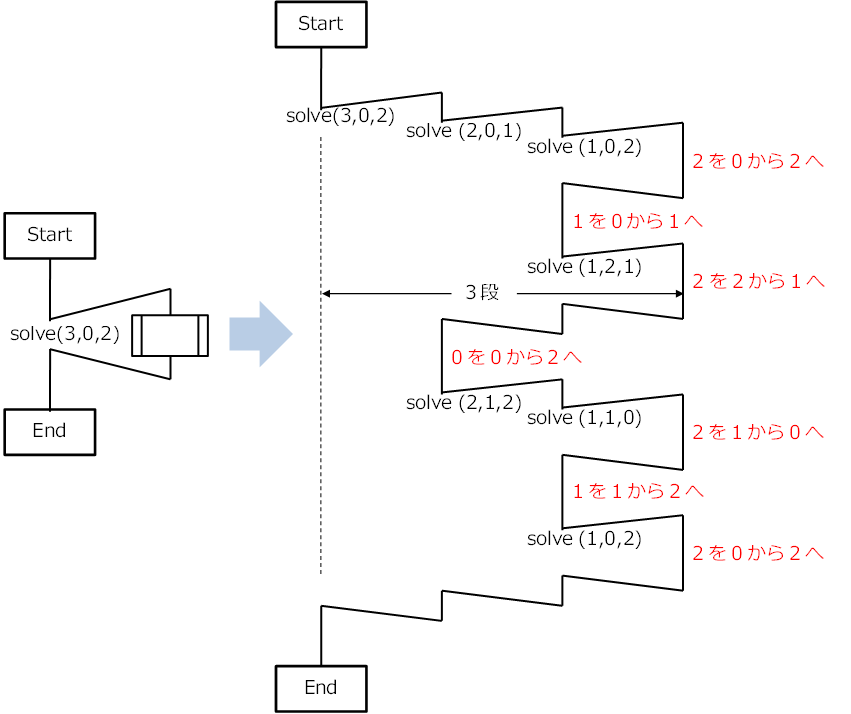
f:id:tfitv:20210223124102p:plain

さらに、円盤がn枚の場合は枚数に比例して深くなり、フラクタル構造になっていることがわかる。

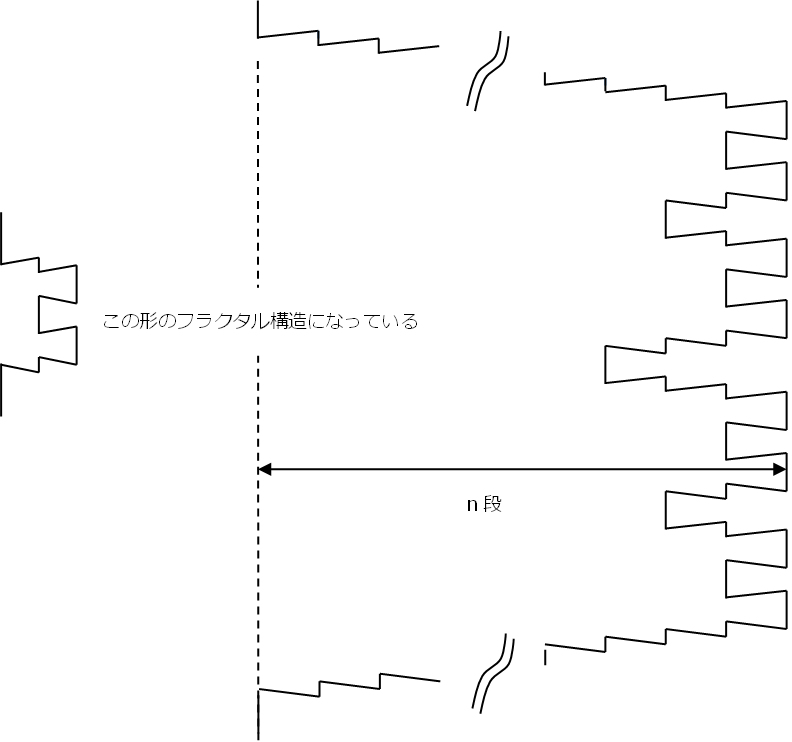
f:id:tfitv:20210223124455p:plain

この図からも円盤が1枚増えるごとに必要な処理の量が2倍になっていくのが推測できるが、n枚の円盤を移すためには何回円盤を移動する必要があるだろうか？ n枚の時に必要な回数を $\displaystyle{ f _ {n} }$ とすると、上述したしたアルゴリズムに従うと

$\displaystyle{ f_{n}=f_{n-1}+1+f_{n-1}=2 f_{n-1}+1 }$

となる。これを変形すると

$\displaystyle{ f_{n}+1=2\left(f_{n-1}+1\right) }$

という形の等比数列になることがわかるので、

$\displaystyle{ f_{n}+1=2\left(f_{n-1}+1\right)=2^{2}\left(f_{n-2}+1\right)=\cdots=2^{n-1}\left(f_{1}+1\right) }$

と変形できる。ここで $\displaystyle{ f _ {1}=1 }$ であるので、それを代入すると

$\displaystyle{ f_{n}+1=2^{n} }$

となり、 $\displaystyle{ f_{n} }$ は、 $\displaystyle{ 2^{n}-1 }$ で計算することができる。ハノイの塔の伝説によれば、64枚の重ねられた円盤を移し終えたときにこの世は終焉を迎えると言われているらしいが、 $\displaystyle{ 2^{64} }$ はそのくらい巨大な数になるのでこの世の終わりと言われても否定することもできない。上の写真で示した今回対象にしているパズルでは $\displaystyle{ n=7 }$ であるので $\displaystyle{ f _ {7}=127 }$ になる。Mindstormsのロボットで1枚動かすのに10秒かかるとすると、要する時間は1270秒で、20分以上はかかる計算になる。

EV3でハノイの塔を　その3　⇔　EV3でハノイの塔を　その５