数独のルールは単純である。
横9マス、縦9マス、3×3のブロック内に同じ数字が入らない、というルールに従って解くとすれば、解法のアルゴリズムは次のような疑似コードで描くことができる。
while 確定したマスの数が81個より少ない: #基本処理 「着目するマスの横、縦、3×3のブロック内の他のマスに確定した数字があれば、 その数字を着目したマスの候補から除く。」 「着目するマスのある候補が、横、縦、3×3のブロック内の他のマスの候補でなければ、 その候補で着目したマスを確定する。」 「着目したマスに候補が一つだけであれば、その数字で確定する。」
簡単な問題であれば、このループを何回か回せば、解くことができる。
実際、ネット上で見つけることができる問題の初級、中級とレベル分けされているものであれば大体これだけで解けるようである。
しかし、上級あるいは難問と記されている問題になると、上述した基本処理ではどうしてもマスの数字を確定できない場合がでてくる。
その場合には、候補の少ないマスのどれかを選択し、そのマスで候補のうちの一つを仮定して、基本方針に従って解き進める。途中でまた候補が絞り切れない状態になった場合は、再度、候補の少ないマスのどれかを適当に選択し、そこで候補のうちの一つを仮定して、基本処理に従って解き進める。
運が良ければそれを続けることによって解けるが、仮定した数字が間違っていた場合には、途中でルールに合わない状態が発生する。例えば、候補が無くなる、あるいは横9、縦9、3×3のブロック内に同じ数字があるといったことである。
その場合には、仮定をした状態に立ち戻り、他の候補の中から一つを選択して仮定して解き進める。
候補がない場合は、その一つ前に仮定した状態に戻して仮定をやり直す。
つまり、図のような木構造を深さ優先で探索すればいいだろう。
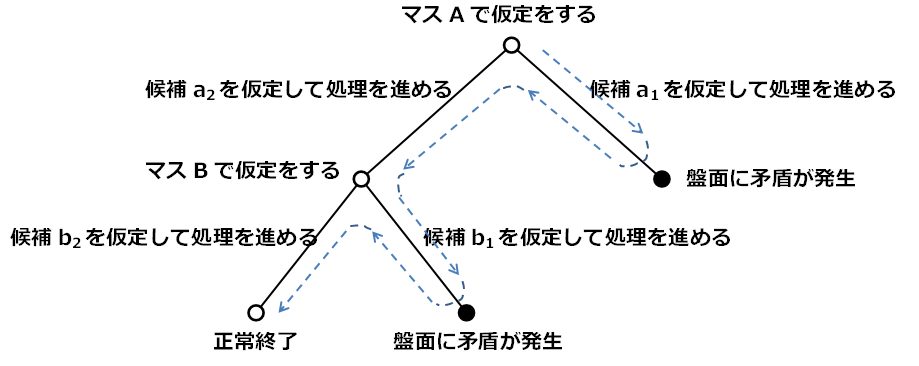
それを、疑似コードで書き下すと下記のようになる。
while 確定したマスの数が81個より少ない: #基本処理 「・・・」「・・・」「・・・」 if 上記の基本処理の結果、確定した数が増えなかった: 仮定を置くマスを決め、候補のうちの一つを仮定する if 盤面がルールに反する: while 仮定をしたマスに他に候補がない: 一つ前に仮定を置いた状態にもどる 仮定をしたマスで新たな候補を選択して仮定する 終了