The Fool In The Valleyの雑記帳

-- 好奇心いっぱいのおじいちゃんが綴るよしなし事 --

トップ > コンピュータ-Mindstorms > Gyrod　【理論編　その１】

Gyrod　【理論編　その１】

コンピュータ-Mindstorms コンピュータ-Python コンピュータ

GyrodはMindstorms EV3で構築した図1のような形状をした2輪のロボットで、バランスを取って直立させながら、遠隔操縦で走行させることができます。

図１　側面図　　正面図
これを実現するうえで最も難しいのが直立させ続けるための制御で、一般に倒立振子として知られる工学的課題です。

ja.wikipedia.org

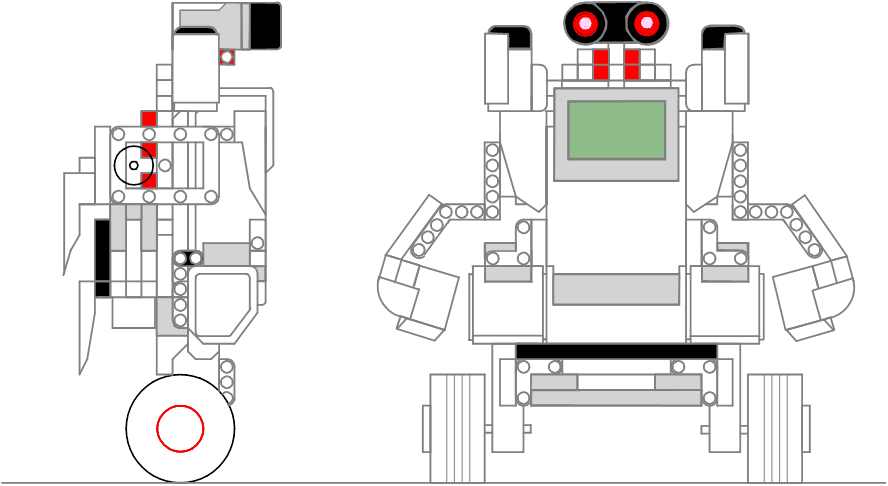
ここではGyrodにおけるその課題の解決方法を説明します。

Gyrodがバランスを取って直立しているとき、重心が少し前にあるので図2左のように少し後傾した形になることが予想されます。しかしその時、Gyrodの車軸の上に乗った部分の重心は車軸の鉛直線上にありますから、図2右のように支点の上に剛体がバランスを取って乗っている簡略化したモデルで考えることができます。

図2　解析のために簡略化したモデル

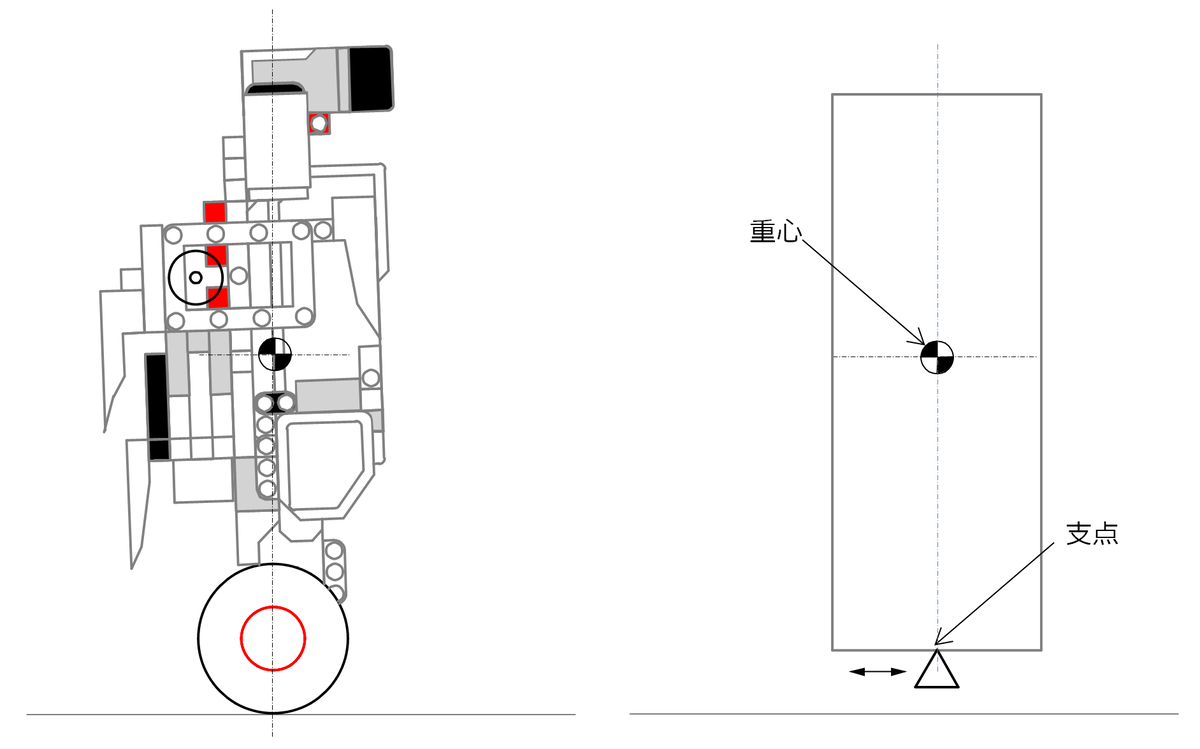
剛体は支点を中心に自由に回転するので、その剛体が傾いたとき、その傾いた方向に支点を水平移動させることによって重心を支点の鉛直上に戻すことにより傾きが正されてバランスをとり続けることができるわけです。Gyrodではそれを実現するために、傾きをジャイロセンサで検出し、支点の水平方向の移動は車軸のモーターの回転で行なうようになっています。 その動きを図 3のように車軸に垂直な面内で考えることにします。今、剛体は一様で質量\displaystyle{M}、長さ\displaystyle{2L}、幅\displaystyle{2L/3}で重心周りの慣性モーメントを\displaystyle{I}とし、車輪は質量\displaystyle{m}、半径\displaystyle{r}とすると、剛体の傾きを \displaystyle{\varphi} 、車輪の位置を\displaystyle{y}とし、支点に水平、垂直にかかる力を\displaystyle{H}、\displaystyle{V}、車輪の回転によって水平方向に与えられる力を\displaystyle{u} とするとき、剛体および車輪にかかる力は図3のようになり、その関係を式で書き表すと(1)~(5)のようになります。

図3　剛体と車輪にかかる力

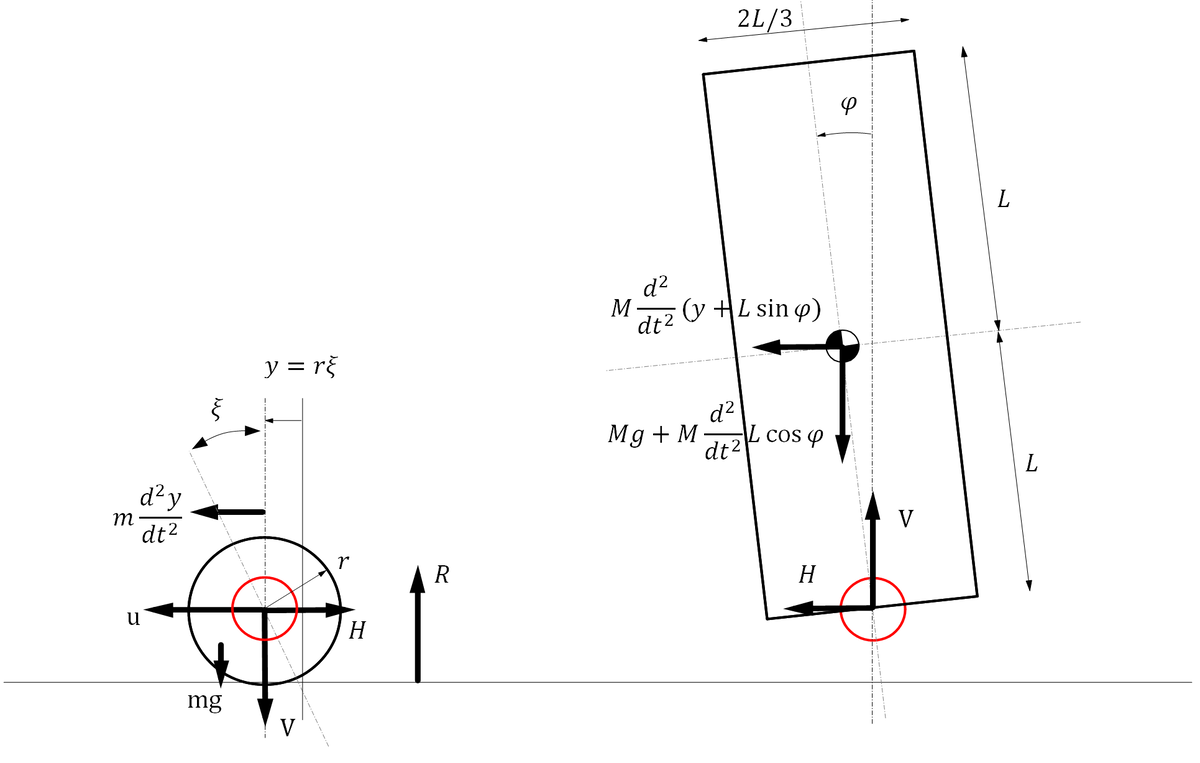
ロボットの重心周りの回転運動

\begin{eqnarray}\displaystyle{
I\frac{d^2 \varphi}{\mathrm{dt}^2}=V L \sin \varphi-H L \cos \varphi
}\end{eqnarray}

ロボットの重心の水平方向の運動

\begin{eqnarray}\displaystyle{
H=M \frac{d^2}{d t^2}(y+L \sin \varphi)
}\end{eqnarray}

ロボットの重心の垂直方向の運動

\begin{eqnarray}\displaystyle{
V=M g+M \frac{d^2}{d t^2} L \cos \varphi
}\end{eqnarray}

車輪の水平方向の運動

\begin{eqnarray}\displaystyle{
u-H=m \frac{d^2 y}{d t^2}
}\end{eqnarray}

車輪の垂直方向の力のつり合い

\begin{eqnarray}\displaystyle{
R=V+mg
}\end{eqnarray}

傾き φ が十分小さい場合、\displaystyle{ \sin \varphi \approx \varphi } 、\displaystyle{ \cos \varphi \approx 1 }　なので、(1)~(4）は次のように書き直すことができます。

\begin{eqnarray}\displaystyle{
I \ddot{\varphi}=V L \varphi-H L
}\end{eqnarray}
\begin{eqnarray}\displaystyle{
H=M \ddot{y}+M L \ddot{\varphi}
}\end{eqnarray}
\begin{eqnarray}\displaystyle{
V=M g
}\end{eqnarray}
\begin{eqnarray}\displaystyle{
u-H=m \ddot{y}
}\end{eqnarray}

この式から中間変数\displaystyle{H}、\displaystyle{V}を消去し、 \displaystyle{\varphi}と\displaystyle{y} の最高階微分について整理すると

\begin{eqnarray}\displaystyle{
\ddot{\varphi}=\frac{(M+m) M L g}{(M+m) I+M m L^2} \varphi-\frac{M L}{(M+m) I+M m L^2} u
}\end{eqnarray}
\begin{eqnarray}\displaystyle{
\ddot{y}=-\frac{M^2 L^2 g}{(M+m) I+M m L^2} \varphi+\frac{I+M L^2}{(M+m) I+M m L^2} u
}\end{eqnarray}

の形の2元連立2階常微分方程式になります。Gyrodは、ジャイロセンサを具備しているので\displaystyle{\dot{\varphi}}が測定でき、その時間積分で\displaystyle{{\varphi}}が求められます。また、車軸の角度　\displaystyle{\xi}　の情報はモーターから得られるのでその時間微分で　\displaystyle{\dot{\xi}}　を求めることができ、それから　\displaystyle{y=r\xi}　、\displaystyle{\dot{y}=r\dot{\xi}}　が計算できるので、\displaystyle{{\varphi}}、\displaystyle{\dot{\varphi}}、\displaystyle{y}、\displaystyle{\dot{y}}　をシステムの状態変数として選び、状態変数ベクトル \displaystyle{\boldsymbol{x}}を

\begin{eqnarray}\displaystyle{
\boldsymbol{x}=\left(\begin{array}{l}
x_1 \\
x_2 \\
x_3 \\
x_4
\end{array}\right)=\left(\begin{array}{l}
\varphi \\
\dot{\varphi} \\
y \\
\dot{y}
\end{array}\right)
}\end{eqnarray}

と設定するのが自然です。 また、制御のための入力は水平方向に与えられる力 \displaystyle{u} のみで、それは車輪のトルクを\displaystyle{{\tau}}とするとき　\displaystyle{{u=\frac{\tau}{r}}}　であり、その \displaystyle{{\tau}} はモーターの駆動電流 で制御できるので、制御ベクトル\displaystyle{\boldsymbol{u}}

\begin{eqnarray}\displaystyle{
\boldsymbol{u}=\left(\begin{array}{l}
u \\
0 \\
0 \\
0
\end{array}\right)
}\end{eqnarray}

はモーターの駆動電流で制御することができます。式を見やすくするために

\begin{eqnarray}\displaystyle{
a=\frac{(M+m) M L g}{(M+m) I+M m L^2} \quad b=-\frac{M^2 L^2 g}{(M+m) I+M m L^2}
}\end{eqnarray}
\begin{eqnarray}\displaystyle{
c=-\frac{M L}{(M+m) I+M m L^2} \quad d=\frac{I+M L^2}{(M+m) I+M m L^2}
}\end{eqnarray}

と置くと、(10)~(15)は

\begin{eqnarray}\displaystyle{
\begin{array}{ll}
\dot{x_1}=  &  x_2 \\
\dot{x_2}=a x_1  &   &   &   \ \ \ \ \ +c u \\
\dot{x_3}=  &  &  &  x_4 \\
\dot{x_4}=b x_1 &  &  & \ \ \ \ \ +d u
\end{array}
}\end{eqnarray}

のような1階の連立微分方程式としてまとめられます。これは状態変数についての連立微分方程式で状態方程式と呼ばれますが、

\begin{eqnarray}\displaystyle{
\boldsymbol{A}=\left(\begin{array}{cccc}
0 & 1 & 0 & 0 \\
a & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
b & 0 & 0 & 0
\end{array}\right) \quad \boldsymbol{B}=\left(\begin{array}{l}
0 \\
c \\
0 \\
d
\end{array}\right)
}\end{eqnarray}

と定義すると(16)の状態方程式は

\begin{eqnarray}\displaystyle{
\dot{\boldsymbol{x}}=\boldsymbol{A} \boldsymbol{x}+\boldsymbol{B}u
}\end{eqnarray}

というすっきりとした形で書き表すことができます。 この状態方程式で表されるシステムを有限時間内に任意の状態から任意の別の状態に遷移させることができることを可制御と言いますが、そのシステムが可制御であるための必要十分条件は、現代制御理論が教えるところによれば、　

\begin{eqnarray}\displaystyle{
\boldsymbol{M}=\left(\begin{array}{llll}
\boldsymbol{B} & \boldsymbol{A} \boldsymbol{B} & \boldsymbol{A}^2 \boldsymbol{B} & \boldsymbol{A}^3 \boldsymbol{B}
\end{array}\right)
}\end{eqnarray}

で定義される４ｘ４の可制御性行列\displaystyle{\boldsymbol{M}}の階数が４あることです。\displaystyle{\boldsymbol{M}}の成分は

\begin{eqnarray}\displaystyle{
\boldsymbol{B}=\left(\begin{array}{l}
0 \\
c \\
0 \\
d
\end{array}\right), \quad \boldsymbol{A} \boldsymbol{B}=\left(\begin{array}{l}
c \\
0 \\
d \\
0
\end{array}\right), \quad \boldsymbol{A}^{\mathbf{2}} \boldsymbol{B}=\left(\begin{array}{c}
0 \\
a c \\
0 \\
b c
\end{array}\right), \quad \boldsymbol{A}^{\mathbf{3}} \boldsymbol{B}=\left(\begin{array}{c}
a c \\
0 \\
b c \\
0
\end{array}\right)
}\end{eqnarray}

であるので

\begin{eqnarray}\displaystyle{
\boldsymbol{M}=\left(\begin{array}{cccc}
0 & c & 0 & a c \\
c & 0 & a c & 0 \\
0 & d & 0 & b c \\
d & 0 & b c & 0
\end{array}\right)
}\end{eqnarray}

となり、それぞれの行ベクトルは明らかに一時独立なので、\displaystyle{\boldsymbol{M}}の階数は４になり、状態方程式で表されるシステムは可制御であることが保証されます。

この制御系を構築する具体的な方法はこれに続く【理論編　その２】で説明します。

→　Gyrod　【理論編　その２】

→　Gyrod　【ソフトウェア編】

→　Gyrod 　【ハードウェア編】